Calcolo dell'Ipotenusa con il Teorema di Pitagora
Cos’è ’Ipotenusa
In un triangolo rettangolo l’ipotenusa è il lato opposto all’angolo retto formato dai due cateti.
In altri termini l’ipotenusa congiunge le estremità dei due cateti e forma con essi due angoli la cui somma è esattamente uguale a 90°.
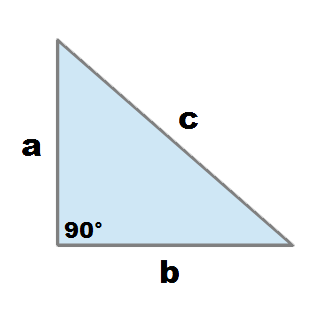
Nella figura "a" e "b" sono i cateti e "c" è l’ipotenusa.
Se il triangolo rettangolo ha due cateti uguali (a = b) allora ciascuno degli angoli formati con l’ipotenusa sarà uguale a 45°.
Come si calcola l’Ipotenusa
La lunghezza dell’ipotenusa di un triangolo rettangolo conoscendo le misure dei suoi cateti si ottiene applicando il noto Teorema di Pitagora.
Il Teorema di Pitagora afferma che:
In un triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti.

L’espressione "quadrato costruito sull’ipotenusa" indica un quadrato il cui lato è esattamente uguale alla lunghezza dell’ipotenusa stessa, come si vede nell’immagine.
Lo stesso vale per i quadrati costruiti sui due cateti.
Poichè l’l’area del quadrato si ottiene moltiplicando il lato del quadrato per sé stesso, che equivale ad elevare il lato alla seconda, possiamo esprimere il teorema di Pitagora con la seguente equazione:
dove:
- c2 è l’area del quadrato costruito sull’ipotenusa "c"
- a2 è l’area del quadrato costruito sul cateto "a"
- b2 è l’area del quadrato costruito sul cateto "b"
da cui, applicando la radice quadrata a entrambi i membri, l’equazione è sempre soddisfatta:
Nota: le parentesi indicano che la radice quadrata va calcolata sul risultato della somma a2 + b2, ossia prima si esegue la somma del quadrato dei due cateti e poi si calcola la radice quadrata.
Dato che la radice quadrata di un numero elevato alla seconda è proprio il numero stesso, ossia √c2 = c, l’equazione diventa:
In altre parole, per calcolare la lunghezza dell’ipotenusa di un triangolo rettangolo conoscendo quella dei suoi cateti, prima si calcolano i quadrati dei due cateti, poi si sommano e si calcola la radice quadrata del risultato della somma.
Esempio di calcolo
Calcolare la lunghezza dell’ipotenusa di un rettangolo i cui cateti misurano 3 e 5 centimetri.
Applicando la formula vista sopra abbiamo:
da cui si ottiene:
Applicazioni pratiche
In geometria il teorema di Pitagora si utilizza spesso per calcolare la diagonale dei parallelepipedi conoscendo le lunghezze dei lati.
Ad esempio, per calcolare la diagonale di un quadrato partendo dalla misura del suo lato, si divide il quadrato in due triangoli rettangoli la cui ipotenusa coincide esattamente con la diagonale del quadrato che vogliamo calcolare ed i cateti non sono altro che i lati del quadrato stesso.
Lo stesso metodo vale naturalmente per il rettangolo: tracciando la diagonale otteniamo sempre due triangoli rettangoli con l’unica differenza che i cateti hanno lunghezze diverse ma vale comunque il teorema di Pitagora per calcolare la diagonale.
