Calcolo Area del Triangolo con la Formula Classica
Cos’è l’area del triangolo
L’area del triangolo è la misura della porzione di piano delimitata da un triangolo.
Il triangolo è una figura geometrica piana composta da tre lati in cui la somma degli angoli interni è pari a 180°
Come si calcola l’Area del Triangolo
L’area del triangolo (equilatero, isoscele, scaleno ecc…) si calcola moltiplicando la base del triangolo per l’altezza relativa alla base.
Per calcolare la superficie di un qualsiasi triangolo si procede come segue:
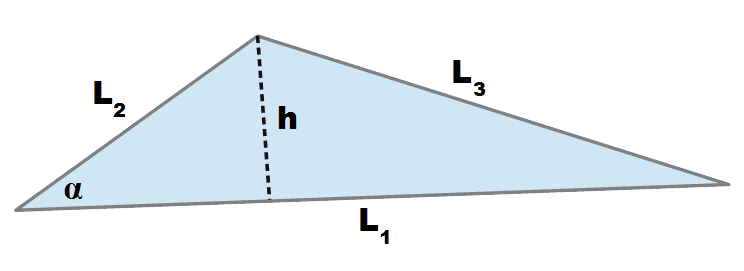
Si sceglie uno dei tre lati del triangolo di cui si conosce la lunghezza e si considera come base (poniamo ad esempio: L1).
Si traccia la perpendicolare h tra la base L1 fino al vertice opposto, ossia fino al punto di congiunzione dei due lati rimanenti (nel nostro caso: L2 e L3), e si misura la sua lunghezza.
Si moltiplica la base L1 per l’altezza h e si divide il risultato per 2.
La formula generica per calcolare l’area del triangolo è quindi:
(base per altezza diviso due)
dove:
- b è la base, ossia uno dei 3 lati del triangolo.
- h è l’altezza perpendicolare alla base che forma con la base un angolo di 90°.
Tale formula è detta anche "formula classica" e presuppone che sia possibile misurare almeno un lato del triangolo e l’altezza perpendicolare ad esso.
Altre formule
Oltre alla formula "classica" appenda vista (base x altezza diviso 2) esistono altre formule per calcolare l’area di un triangolo.
La Formula di Erone
La formula di Erone si utilizza quando si conoscono le lunghezze dei tre lati ma per varie ragioni non si è in grado di misurare l’altezza del triangolo a partire da uno dei lati.
Per maggiori informazioni e per il calcolo basato sulla formula di Erone si rimanda all’ apposita applicazione.
Trigonometria
Un’altra formula che può risultare utile anche nella pratica è basata sulla trigonometria e si utilizza quando si conoscono le lunghezze di due lati e l’ampiezza dell’angolo da essi formato, ossia dell’angolo compreso tra i due lati.
Tale formula asserisce che l’area di un rettangolo è il prodotto di due lati per il seno dell’angolo tra essi compreso, il tutto diviso 2.
Con riferimento alla figura precedente abbiamo che:
dove:
- L1 e L2 sono le lunghezze di due lati del triangolo.
- α è l’angolo formato dai due lati.
- in trigonometria "sen α" indica l’operazione di calcolo del "seno" di α.
Il Triangolo Rettangolo
Un caso particolare è costituito dal triangolo rettangolo.
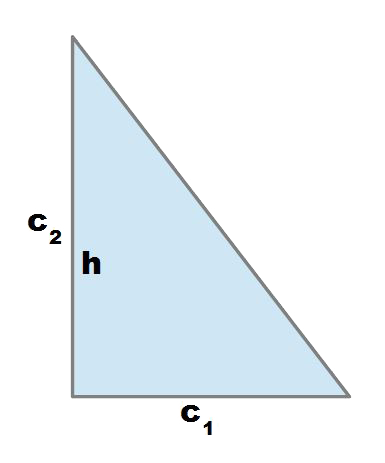
Poiché il triangolo rettangolo è un triangolo in cui due lati, detti cateti, sono perpendicolari tra loro, se consideriamo come base uno dei due cateti (ad esempio c1 nell’immagine), l’altezza h sarà sempre la misura dell’altro cateto (c2) proprio per la definizione stessa di altezza che, come detto, è perpendicolare alla base e in questo caso coincide esattamente con l’altro cateto.
L’area di un triangolo rettangolo può essere espressa quindi come prodotto dei cateti diviso due.
dove:
- c1 e c2 sono le misure dei cateti.
In altri termini, per misurare l’area di un triangolo rettangolo, basta conoscere le misure dei suoi cateti e non è necessario tracciare l’altezza e misurarla.
Nota:
Se i cateti hanno lughezze diverse si parla anche di "cateto minore" e "cateto maggiore".
Se i due cateti sono uguali, il triangolo rettangolo è anche isoscele.
Esempi di calcolo
Calcolare l’area di un triangolo avente una base di 10,8 metri ed un’altezza di 3,75 metri arrotondando il risultato a due decimali.
Poiché conosciamo sia la base che l’altezza, possiamo applicare la formula classica:
da cui si ottiene:
