Calcola la Diagonale del Quadrato
Cos’è la diagonale di un quadrato
La diagonale del quadrato è la linea retta che congiunge i vertici opposti del quadrato.
La diagonale divide il quadrato in due triangoli rettangoli uguali i cui cateti sono i lati adiacenti del quadrato (L) e l’ipotenusa è la diagonale (d).
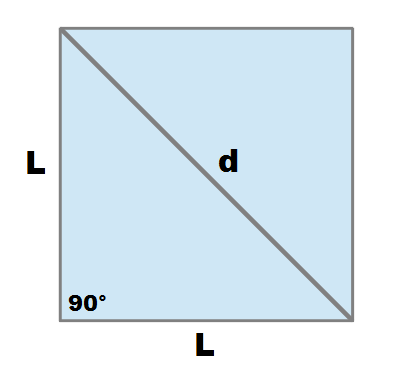
Esistono in pratica due diagonali per ciascun quadrato ed esse si intersecano nel centro del quadrato stesso, dividendolo in quattro triangoli rettangoli uguali.
Come si calcola la diagonale di un quadrato
Come si vede dall’immagine, la diagonale del quadrato (d) concide con l’ipotenusa dei due triangoli rettangoli, e pertanto, per calcolare la sua lunghezza, possiamo avvalerci del noto teorema di Pitagora.
Grazie al teorema di Pitagora è possibile calcolare la lunghezza dell’ipotenusa conoscendo quella dei suoi cateti, che in questo caso coincidono con i lati del quadrato (L), e pertanto il gioco è fatto.
La formula semplificata
Esiste una formula semplificata che deriva da quella ricavata tramite il teorema di Pitagora e che tiene conto che, nel caso del quadrato, i cateti dei due triangoli formati dalla diagonale sono uguali.
Partiamo dalla formula generica per il calcolo dell’ipotenusa 'c' dati i due cateti 'a' e 'b':
Poiché nel nostro caso la diagonale 'd' è la nostra ipotenusa 'c' e i cateti 'a' e 'b' sono entrambi uguali a 'L' (il lato del quadrato), possiamo scrivere:
Per la proprietà della radice quadrata applicata ad un prodotto abbiamo:
da cui:
In altri termini, per calcolare la lunghezza della diagonale di un quadrato conoscendo quella del lato, basta moltiplicare il lato per la radice quadrata di 2, ossia per il valore costante 1,414213562373095…
Esempi di calcolo
Calcolare la diagonale di un quadrato il cui lato misura 5 metri.
Applichiamo la formula derivata dal teorema di Pitagora:
da cui si ottiene:
Analogamente, applicando la formula semplificata, abbiamo:
